Inserción en modelo de conjuntos anidados.

Anteriormente se comentó cómo almacenar en tablas de una base de datos información que presente jerarquía entre ella, proponiendo el modelo de conjuntos anidados como una estructura más compacta y más operativa.
Como se comentó, Joomla 2.5 usa este modelo ( en su tabla #__asset ) para almacenar información estableciendo jerarquías entre la misma. Si tratamos de desarrollar un componente para Joomla 2.5 que importe información masiva, desde por ejemplo un fichero CSV, deberemos comprender cual es la operativa con este tipo de tablas, ya que de no calcularse adecuadamente los índices de cada nuevo elemento lo más probable es que la información almacenada en la base de datos no pueda estar disponible para el gestor de contenidos. Esto mismo es extensible para cualquier tipo de software que tenga que acceder a este tipo de tablas.

Veremos ahora cual sería el mecanismo de inserción en este tipo de árboles y como se verían reflejadas estas modificaciones en su correspondiente representación en tablas.

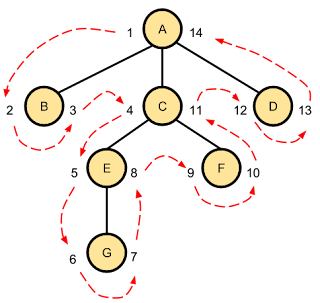
Tenemos por ejemplo esta estructura de contenidos representada tanto por su árbol de jerarquías como por la tabla que lo almacena.

• 

• Item	lft	rgt
  A	1	14
  B	2	3
  C	4	11
  D	12	13
  E	5	8
  F	9	10
  G	6	7

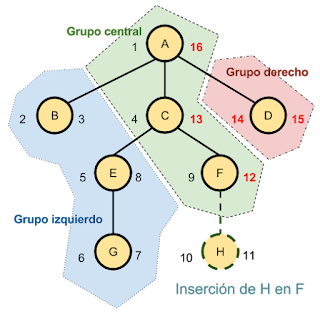
Supongamos que queremos insertar un nuevo nodo, H. ¿Cómo se verían afectados los índices ya establecidos en la tabla?

• 

• Item	lft	rgt
  A	1	16
  B	2	3
  C	4	13
  D	14	15
  E	5	8
  F	9	12
  G	6	7
  H	10	11

Para calcular los valores de los nodos se ha efectuado un recorrido en profundidad en el árbol. Pero vemos que no todos los nodos han tenido que modificar sus índices al insertar en nuevo nodo. Podemos diferenciar tres grupos tomando como referencia un nodo, en este caso el insertado:

• grupo izquierdo: estos no ven modificados ninguno de sus índices.
• grupo central: todos los ancestros del nodo. Sólo incrementan en 2 su valor rgt.
• grupo derecho: incrementan en 2 los valores lft y rgt.

Ya que ilustraremos los ejemplos con código php, podemos formalizar la definición de estos grupos en base a las propiedades de sus índices con respecto al nodo que tomamos como referencia.

Tomemos que este nuevo nodo esta definido como:

   public class nodoLR {
      public lft; 
      public rgt; 
      public item; 
   } 
   public class arbolLR {  ...  }   
   $arbol = new arbolLR(...); 
   $nodo = new nodoLR();  
   $nodo->lft= 10; 
   $nodo->rgt=11; 
   $nodo->item='H';

Las propiedades lft y rft del nodo las hemos asignado directamente en este ejemplo.  En una inserción deduciríamos estos valores en función del nodo padre en el que insertaremos el nuevo nodo.
En base a estas propiedades que acabamos de comentar, clasificaremos el resto de nodos del árbol con respecto al nuevo nodo siguiendo los criterios que indicamos a continuación.

• Un nodo A es del grupo izquierdo si tiene valores lft y rgt menores:
  ($nodoA->lft < $nodo->lft) && ($nodoA->rgt < $nodo->rgt)
• Un nodo A es del grupo central si lft es menor, pero rgt es mayor:
  ($nodoA->lft < $nodo->lft) && ($nodoA->rgt > $nodo->rgt)
• Un nodo A es del grupo derecho si tanto lft como rgt son mayores:
  ($nodoA->lft > $nodo->lft) && ($nodoA->rgt > $nodo->rgt)

Teniendo en cuenta estas características que hemos deducido, la actualización de la tabla que representa esta estructura será muy sencilla, más si la comparamos con la implementación padre - hijo que vimos anteriormente. De hecho, aunque por el momento no se entrará a estudiar este caso, es muy posible que la implementación padre - hijo al basarse en una serie de relaciones encadenadas entre elementos no permita resolver operaciones de búsqueda e inserción exclusivamente mediante SQL. Podría requerir la ejecución de código iterativo o recursivo, incrementando el coste de ejecución sensiblemente.

La operación de inserción de un elemento implicará:

• actualizar todos los nodos del grupo central sumando 2 al valor rgt
• actualizar todos los nodos del grupo derecho sumando 2 al valor lft y rgt
• insertar el nuevo nodo con los índices correspondientes

En primer lugar, aunque la inserción en la tabla será la última operación a realizar, tendremos que calcular primero los índices del elemento a insertar para, en base a ellos, realizar las actualizaciones.
Habrá que calcular los índices a partir de los del padre, pero si no es el único hijo habrá que calcularlos a partir del hermano más próximo. Tendremos en cuenta que las inserciones se realizan siempre por la derecha, de tal forma que el último hermano insertado siempre será el que tenga los ínidices con valores más altos.

Si los valores del padre son consecutivos, es decir
                 $padre->lft == $padre->rgt+1;
tendremos la certeza de que este es un nodo terminal y por lo tanto
                  $nodo->lft=$padre->lft+1;
                  $nodo->rgt=$padre->lft+2;

Si esta condición no se cumple entonces tendremos que calcular el valor a partir del último hijo existente. Tendremos en cuenta que la inserción será al nivel inmediatamente inferior al padre. Podremos asegurar con total certeza que, dado que la asignación de índices se realiza en función del recorrido en profundidad en el árbol, existirá un hijo, cuyo valor rgt será $padre->rgt-1 y además este será el último de todos sus hijos.

También sabemos que si
                 ($nodo1->rgt+1 == $nodo2->lft)
podremos asegurar que $nodo1 y $nodo2 están al mismo nivel. De esta forma, si el nodo padre no es terminal, con lo visto deducimos que
                  $nodo->lft = $padre->rgt  y $nodo->rgt=$padre->rgt+1

Con lo visto hasta ahora el algoritmo para calcular el valor del hijo a insertar podría ser este:

  if($padre->lft+1 == $padre->rgt){ //padre es nodo terminal
    $nodo->lft=$padre->lft+1; 
    $nodo->rgt=$padre->lft+2;
  } 
  else {
    $nodo->lft = $padre->rgt; 
    $nodo->rgt=$padre->rgt+1;
  }
 De esta forma podemos escribir las sentencias SQL que actualizarían los valores de la tabla donde está almacenado el árbol.
Para los nodos centrales:

//actualización de todos los nodos centrales 
 UPDATE tabla
 SET rgt=rgt+2
 WHERE lft<=$padre->lft
 AND rgt>=$padre->rgt

Y para los nodos del grupo derecho:

//actualización de todos los nodos del grupo derecho
 UPDATE tabla 
 SET lft=lft+2, rgt=rgt+2 
 WHERE lft>$padre->lft 
 AND rgt>$padre->rgt

Por último quedaría insertar el nuevo nodo, cuyos valores ya hemos calculado.

 INSERT INTO tabla 
 VALUES ($nodo->item,$nodo->lft,$nodo->rgt)

Aunque hemos mostrado el proceso de inserción de un único nodo, lo cierto es que sería posible la inserción de un conjunto de nodos hermanos. Tomarían valores lft y rgt consecutivos, encadenados entre nodo y la actualización del resto del árbol sería análoga, multiplicando 2 por el número de nodos insertados.