Tratamiento de select multiple y paso de arrays por $_POST

Mediante un formulario podemos enviar información a un script para que la procese. Habitualmente esta información es la que proviene directamente de los mismos campos del formulario.
Cuando el usuario introduce la información cada elemento del formulario se procesa, creando una variable con el atributo 'name' con el valor indicado en el atributo 'value'.
El problema surge cuando nos vemos con la necesidad de enviar datos algo más complejos que un simple valor, como por ejemplo un conjunto de valores en una variable, como un array o información más estructurada.
Tomemos un ejemplo sencillo. Un usuario puede acceder desde una web múltiples productos de una oferta. Esta selección se procesará. Si cumple una serie de condiciones se pasará otro formulario de confirmación para posteriormente aplicar descuentos, y si no de vuelta al principio.
Este sería el punto de entrada:

<form name="pedido" method="post" action="procesar.php">
<label for="tfno"> Tfno </label>
<input name="tfno" type="text"></input>
<label for="ofertas[]">Ofertas</label>
<select name="ofertas[]" multiple>
    <option value="100">Pizza</value>
    <option value="101">Bocata</value>
    <option value="102">Ensalada</value>
    <option value="103">Kebab</value>
    <option value="110">Refresco</value>
   //... más opciones
</select>
<input type="submit" value="Procesar"></input>
</form>

Se puede comprobar que  el name del select se ha definido como ofertas[], con corchetes. Si la variable la pasamos por GET en la URL veríamos una sucesión de parámetros con el mismo nombre, uno por cada selección y podríamos procesar esta cadena. Pero al ser por POST sólo obtendremos el último valor de todos los seleccionados.
De esta forma lo que obtenemos será un array que procesará en este caso el script 'procesar.php'

$ofertas=$_POST['ofertas'];
//...
 foreach ($ofertas as $oferta) {
       $importe_total += precio($oferta);
//...tratamiento de cada código de producto
}

Este script hará una serie de cálculos sobre el array recibido, por ejemplo una validación. Una vez hecha, supongamos que se requiere de otro formulario más para que el usuario haga una serie de confirmaciones o aporte más datos.
Por ejemplo, se ha verificado que el pedido es correcto, que la selección se ajusta a las condiciones de la oferta y ahora se quiere aplicar un descuento sobre el mismo, visualizándose en un ticket como documento final. Tendremos que pasar el array $ofertas de alguna manera como parámetro al siguiente formulario. Lo haremos de la siguiente manera:

'<input type="hidden" name="ofertas" value="'
       .base64_encode(serialize($ofertas))
       .'" />';           

Es decir, podemos pasar un array serializándolo. Se puede observar que el paso de parámetros se hace en un input oculto, una forma muy habitual de pasar información entre formularios.
Si no usamos la codificación base64 podemos encontrarnos con un error similar al siguiente.

       Error at offset 9 of 13 bytes

La codificación base64 nos garantiza que la información no se verá afectada por los protocolos de transporte.
De forma análoga, estos datos enviados serializados y codificados al recibirse podrán ser usados tras descodificarse y deserializarse. Por ejemplo, en facturar.php recibiriamos los datos de procesar.php para determinar según los productos que descuento aplicar, cual sale gratis, que regalo dar, o lo que fuere oportuno.

$ofertas=unserialize(base64_decode($_POST['ofertas']));
foreach ($ofertas as $oferta) {
     //... tratamiento de cada producto
}

De esta forma, a modo de resumen:

• para recoger variables multivaluadas en un select usar [] en la variable
• para enviar como parámetro POST un array, serializar y codificar en base64

  (base64_encode(serialize($array))

INSERT y UPDATE condicionales en MySQL

En un proceso de importación de datos en el que deseemos fusionar la información existente con la que contiene nuestro fichero, tendremos la necesidad de actualizar o insertar según dicha información esté o no referenciada en la base de datos.
Supongamos que tenemos esta sencilla tabla en la que almacenamos títulos de libros, junto con una puntuación (que vendría a ser la suma de votos que da un usuario que accede al sitio)

id	title	points
1	Alicia en el País de las Maravillas	358
2	El Color de la Magia	324
3	Hamlet	321

Supongamos que el usuario escribe un título que envía al sistema. Si este libro se encuentra se incrementará e uno su puntuación (points). Si no es así se registrará el nuevo libro y se asignará el valor de puntuación a 1.

En principio suele abordarse este tipo de acciones con dos tareas:

• Comprobar si existe el elemento
• Ejecutar acción en base de datos en función de lo anterior

Es decir, la implementación exigiría realizar dos consultas consecutiva.El código para ilustrar como sería esta implementación (usando PHP y el framework de Joomla en este caso) podría ser:

    $db=new JFactory::getDBO();
    //comprobamos si existe el item
    $sql1='SELECT id,title,points
           FROM books
           WHERE title = "$titulo"';
    $db->setQuery($sql1);
    $resultado=$db->loadObjectList();

    //INSERT o UPDATE en función del resultado anterior
    if (empty($resultado)) {//libro no registrado; lo guardamos
        $sql2='INSERT INTO books 
              (title,points) VALUES 
              ("$titulo)","1");';
    }
    else {//el libro está; incrementamos su puntuación
        $sql2='UPDATE books SET points=points+1';
    }
    $db->setQuery($sql2);
    $db->query();

Tenemos que recurrir en este caso a PHP, como podría haber sido a otro lenguaje, para tomar una decisión de que consulta enviar al servidor de base de datos.
En este caso tenemos en mente MySQL.
Podremos resolver esto de otra forma más eficiente usando exclusivamente consultas, ahorrando así en líneas de código, consiguiendo una acción más portable a otros lenguajes y sobretodo ahorrando en tiempo de ejecución.
Hemos planteado el ejemplo con una única inserción, pero en el caso de tener que ejecutar miles de acciones de este tipo la diferencia de tiempo puede ser drástica (más si tenemos en cuenta el problema de tiempo de ejución máxima que tiene un script php en el servidor).
En primer lugar, puede que necesitemos permisos para modificar la estructura de la tabla con la que estamos trabajando, ya que necesitamos especificar que el título del libro va a ser un valor único, es decir, no permitimos el registro de varios libros con el mismo título.
Para ello ejecutamos la siguiente consulta (si es que el diseñador de la base de datos no lo ha tenido en cuenta...)

ALTER TABLE `books` ADD UNIQUE (`title`);

Tras esto podremos realizar operaciones de inserción o actualización automática en el caso de que el item esté, usando una única consulta con ON DUPLICATE KEY:

INSERT INTO `books` (`title`, `points`)
VALUES ('el color de la magia','1')
ON DUPLICATE KEY
UPDATE `points`=`points`+1

Como dato a tener en cuenta (al menos según el cotejamiento de la BD) en el caso del ejemplo si otro usuario pretende insertar 'EL COLOR DE LA MAGIA' se activará ON DUPLICATE KEY, incrementándose el valor points en lugar de insertarse otro nuevo registro.
No se toman en cuenta las mayúsculas y minúsculas, lo cual en este caso no nos viene del todo mal, pero sí que podría ser necesario diferenciar en otros.
De cualquier forma, normalizar previamente el dato a tratar con la base de datos nos ayudará a tener un mayor control en este aspecto.

Inserción en modelo de conjuntos anidados.

Anteriormente se comentó cómo almacenar en tablas de una base de datos información que presente jerarquía entre ella, proponiendo el modelo de conjuntos anidados como una estructura más compacta y más operativa.
Como se comentó, Joomla 2.5 usa este modelo ( en su tabla #__asset ) para almacenar información estableciendo jerarquías entre la misma. Si tratamos de desarrollar un componente para Joomla 2.5 que importe información masiva, desde por ejemplo un fichero CSV, deberemos comprender cual es la operativa con este tipo de tablas, ya que de no calcularse adecuadamente los índices de cada nuevo elemento lo más probable es que la información almacenada en la base de datos no pueda estar disponible para el gestor de contenidos. Esto mismo es extensible para cualquier tipo de software que tenga que acceder a este tipo de tablas.

Veremos ahora cual sería el mecanismo de inserción en este tipo de árboles y como se verían reflejadas estas modificaciones en su correspondiente representación en tablas.

Tenemos por ejemplo esta estructura de contenidos representada tanto por su árbol de jerarquías como por la tabla que lo almacena.

• 

• Item	lft	rgt
  A	1	14
  B	2	3
  C	4	11
  D	12	13
  E	5	8
  F	9	10
  G	6	7

Supongamos que queremos insertar un nuevo nodo, H. ¿Cómo se verían afectados los índices ya establecidos en la tabla?

• 

• Item	lft	rgt
  A	1	16
  B	2	3
  C	4	13
  D	14	15
  E	5	8
  F	9	12
  G	6	7
  H	10	11

Para calcular los valores de los nodos se ha efectuado un recorrido en profundidad en el árbol. Pero vemos que no todos los nodos han tenido que modificar sus índices al insertar en nuevo nodo. Podemos diferenciar tres grupos tomando como referencia un nodo, en este caso el insertado:

• grupo izquierdo: estos no ven modificados ninguno de sus índices.
• grupo central: todos los ancestros del nodo. Sólo incrementan en 2 su valor rgt.
• grupo derecho: incrementan en 2 los valores lft y rgt.

Ya que ilustraremos los ejemplos con código php, podemos formalizar la definición de estos grupos en base a las propiedades de sus índices con respecto al nodo que tomamos como referencia.

Tomemos que este nuevo nodo esta definido como:

   public class nodoLR {
      public lft; 
      public rgt; 
      public item; 
   } 
   public class arbolLR {  ...  }   
   $arbol = new arbolLR(...); 
   $nodo = new nodoLR();  
   $nodo->lft= 10; 
   $nodo->rgt=11; 
   $nodo->item='H';

Las propiedades lft y rft del nodo las hemos asignado directamente en este ejemplo.  En una inserción deduciríamos estos valores en función del nodo padre en el que insertaremos el nuevo nodo.
En base a estas propiedades que acabamos de comentar, clasificaremos el resto de nodos del árbol con respecto al nuevo nodo siguiendo los criterios que indicamos a continuación.

• Un nodo A es del grupo izquierdo si tiene valores lft y rgt menores:
  ($nodoA->lft < $nodo->lft) && ($nodoA->rgt < $nodo->rgt)
• Un nodo A es del grupo central si lft es menor, pero rgt es mayor:
  ($nodoA->lft < $nodo->lft) && ($nodoA->rgt > $nodo->rgt)
• Un nodo A es del grupo derecho si tanto lft como rgt son mayores:
  ($nodoA->lft > $nodo->lft) && ($nodoA->rgt > $nodo->rgt)

Teniendo en cuenta estas características que hemos deducido, la actualización de la tabla que representa esta estructura será muy sencilla, más si la comparamos con la implementación padre - hijo que vimos anteriormente. De hecho, aunque por el momento no se entrará a estudiar este caso, es muy posible que la implementación padre - hijo al basarse en una serie de relaciones encadenadas entre elementos no permita resolver operaciones de búsqueda e inserción exclusivamente mediante SQL. Podría requerir la ejecución de código iterativo o recursivo, incrementando el coste de ejecución sensiblemente.

La operación de inserción de un elemento implicará:

• actualizar todos los nodos del grupo central sumando 2 al valor rgt
• actualizar todos los nodos del grupo derecho sumando 2 al valor lft y rgt
• insertar el nuevo nodo con los índices correspondientes

En primer lugar, aunque la inserción en la tabla será la última operación a realizar, tendremos que calcular primero los índices del elemento a insertar para, en base a ellos, realizar las actualizaciones.
Habrá que calcular los índices a partir de los del padre, pero si no es el único hijo habrá que calcularlos a partir del hermano más próximo. Tendremos en cuenta que las inserciones se realizan siempre por la derecha, de tal forma que el último hermano insertado siempre será el que tenga los ínidices con valores más altos.

Si los valores del padre son consecutivos, es decir
                 $padre->lft == $padre->rgt+1;
tendremos la certeza de que este es un nodo terminal y por lo tanto
                  $nodo->lft=$padre->lft+1;
                  $nodo->rgt=$padre->lft+2;

Si esta condición no se cumple entonces tendremos que calcular el valor a partir del último hijo existente. Tendremos en cuenta que la inserción será al nivel inmediatamente inferior al padre. Podremos asegurar con total certeza que, dado que la asignación de índices se realiza en función del recorrido en profundidad en el árbol, existirá un hijo, cuyo valor rgt será $padre->rgt-1 y además este será el último de todos sus hijos.

También sabemos que si
                 ($nodo1->rgt+1 == $nodo2->lft)
podremos asegurar que $nodo1 y $nodo2 están al mismo nivel. De esta forma, si el nodo padre no es terminal, con lo visto deducimos que
                  $nodo->lft = $padre->rgt  y $nodo->rgt=$padre->rgt+1

Con lo visto hasta ahora el algoritmo para calcular el valor del hijo a insertar podría ser este:

  if($padre->lft+1 == $padre->rgt){ //padre es nodo terminal
    $nodo->lft=$padre->lft+1; 
    $nodo->rgt=$padre->lft+2;
  } 
  else {
    $nodo->lft = $padre->rgt; 
    $nodo->rgt=$padre->rgt+1;
  }
 De esta forma podemos escribir las sentencias SQL que actualizarían los valores de la tabla donde está almacenado el árbol.
Para los nodos centrales:

//actualización de todos los nodos centrales 
 UPDATE tabla
 SET rgt=rgt+2
 WHERE lft<=$padre->lft
 AND rgt>=$padre->rgt

Y para los nodos del grupo derecho:

//actualización de todos los nodos del grupo derecho
 UPDATE tabla 
 SET lft=lft+2, rgt=rgt+2 
 WHERE lft>$padre->lft 
 AND rgt>$padre->rgt

Por último quedaría insertar el nuevo nodo, cuyos valores ya hemos calculado.

 INSERT INTO tabla 
 VALUES ($nodo->item,$nodo->lft,$nodo->rgt)

Aunque hemos mostrado el proceso de inserción de un único nodo, lo cierto es que sería posible la inserción de un conjunto de nodos hermanos. Tomarían valores lft y rgt consecutivos, encadenados entre nodo y la actualización del resto del árbol sería análoga, multiplicando 2 por el número de nodos insertados.

Información jerárquica en bases de datos: lft y rgt.

Los contenidos de una web, y un sistema de información en general, se estructuran de forma lógica en categorías. Dichas categorías pueden ser englobadas por otras de rango superior, o por otro lado, pueden dar pie a otras categorías derivadas.
Dicha lógica debe ser plasmada en un diseño de base de datos. Una implementación intuitiva sería establecer relaciones padre - hijo en cada registro. Nos será sencilla de comprender, pero sus operaciones quizá sean complejas de implementar por los desarrolladores.


En Joomla 2.5 se utiliza un mecanismo para gestionar la jerarquía de la información en la base de datos. En la tabla #__asset se incluye información adicional para cada item del gestor de contenidos, destacando dos campos: lft y rgt. A continuación se comentarán dos modelos para gestionar información jerarquizada en tablas: el modelo de listas de adyacencia (padre - hijo) y el modelo de conjuntos anidadoss (lft - rgt).

Modelo de listas de adyacencia. Implementación padre - hijo

En general nuestras bases de datos almacena información estructurada en una serie de registros. Dichos registros además pueden presentar diversas jerarquías. A nivel lógico resulta intuitiva una visión de estas jerarquías en forma de árboles, la cual deberá implementarse posteriormente en una tabla en la base de datos.

• 

• Item	Padre	Hijo
  A	-	B
  A	-	C
  A	-	D
  B	A	-
  C	A	-
  D	A	-

La implementación de esta jerarquía en una tabla de relaciones es quizá la que a priori parece más intuitiva y lógica a seguir, ya que en una base de datos relacional lo habitual es que relacionemos items por medio de sus claves.
Esta forma de implementar un árbol jerárquico implica cierta redundancia de información como podemos observar en la tabla anterior.
En el caso de insertar un elemento implica además de añadir un nuevo registro (indicando el padre y valor nulo para hijo), actualizar o insertar (para el caso de que haya más hijos) el nuevo nodo hijo en el item padre.

• 

• Item	Padre	Hijo
  A	-	B
  A	-	C
  A	-	D
  B	A	-
  C	A	E
  D	A	-
  E	C	-

En el caso de otras operaciones tales como un recorrido en profundidad de todos los hijos de un nodo padre, partiendo de la estructura de tabla propuesta, reviste cierta complejidad. Tendríamos que, dado un padre, deducir sus descendientes directos, y a su vez por cada uno de ellos realizar la misma operación, así sucesivamente hasta llegar a los nodos terminales que no tengan más descendencia.

Otro problema que presenta la esta implementación es que si quisiéramos establecer algún orden deberíamos añadir información adicional. Es decir, en el gráfico vemos que B, C y D derivan de A. Pero ¿qué orden existe entre ellos? Podría ser D,C, B o cualquier otro, porque la tabla en sí no nos da información que nos lleve a dibujar de forma unívoca un único árbol. Tendríamos que incluir un nuevo campo en la tabla o seguir algún tipo de convención.

Se puede ampliar la información y entrar en  un estudio de mayor profundidad sobre este tipo de implementación en The Adjacency List Model for Trees, de Joe Celko.

Modelo de conjuntos anidados. Implementación left - right.

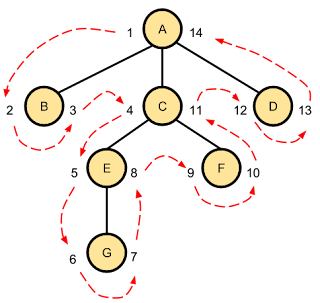
Otra forma de organizar la información de un árbol para facilitar su almacenamiento en tablas es definir por cada nodo dos índices: lft y rgt, haciendo referencia a left (izquierda) y right(derecha). Estos valores representarán el orden de recorrido en profundidad de los nodos del árbol que representa nuestra información jerarquizada.

• 

• Item	lft	rgt
  A	1	8
  B	2	3
  C	4	5
  D	6	7

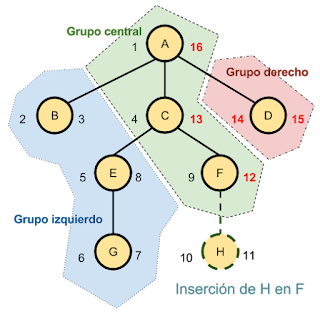
Como se muestra en el gráfico, la asignación de valores es sencilla y la tabla que recoge esta información es compacta. Las inserciones tampoco revisten mayor complejidad, pero como veremos, pueden llegar a verse afectados todos los nodos, ya que en el peor de los casos puede requerir una reindexación total del árbol.

• 

• Item	lft	rgt
  A	1	10
  B	2	3
  C	4	7
  D	8	9
  E	5	6

Esta necesidad de cálculo y actualización puede significar incrementar el coste de añadir información a dicho árbol, así que habrá que analizar si podemos partir de supuestos que nos simplifiquen esta gestión tanto como sea posible. Analizaremos las caracterisiticas y propiedades de esta implementación para comprobar así que motivos justifican su uso frente a la propuesta anterior.

Detección de nodos terminales

Podemos verificar que, dadas las propiedades de este árbol, todo nodo final tiene valores lft y rgt consecutivos. Por ejemplo si un nodo n tiene valores tales como

        $node->lft=i y $node->rgt=i+1

podemos asegurar que no tiene hijos y es por tanto un nodo terminal.

Cálculo de nodos del (sub)árbol.

Otra propiedad de este tipo de árbol es que podemos calcular inmediatamente el número de nodos totales a partir del nodo cima, siendo este valor rgt/2 (tomando que lft comienza en 1). Sí sólo hay un elemento el valor rgt puede ser null y será un caso excepcional.

De hecho podemos extender esta propiedad a cualquier nodo para saber cuantos nodos derivan de un padre, incluído el mismo, siendo este valor

            (rgt-lft)/2 redondeando al entero superior 

Por ejemplo un nodo con valores

            lft=7 y rgt=12

tendríamos que

            (12-7)/2=2.5 

aproximando al entero superior daría 3 , lo que nos indicaría que ese nodo es la cima de un árbol que tiene 3 nodos, incluido él mismo

Mecanismo de inserción.

También podemos comprobar que la inserción de un elemento nunca implica incrementar el valor lft de sus ancestros, aunque sí requiere actualizar este valor en los hermanos de los ancestros más "jóvenes", es decir, los que tengan un valor lft superior al del nodo insertado, es decir, los que se sitúan en la parte derecha del árbol a partir de él.
Además, dado que la inserción del nuevo elemento implica añadir dos nuevos valores (lft y rgt) el incremento que haremos siempre será de 2 en los atributos de dichos nodos.
Los nodos implicados en la actualización siempre serán los superiores y los que se situen a la derecha. Si son ancestros sólo incrementaremos en 2 su valor rgt, dejando tal cual su valor lft. Si no lo son y están a la derecha incrementaremos en 2 sus valores lft y rgt.

Nodos ancestros.

Un nodo es ancestro de otro si su valor lft es menor que el que estamos tomando en consideración. De esta forma si estamos definiendo una serie de categorías jerarquizadas para los elementos de nuestra base de datos, nos será muy sencillo deducir en que categorías está englobado.

Nodos al mismo nivel.

También podemos deducir otras propiedades del árbol fácilmente, como por ejemplo los nodos que están a un mismo nivel de profundidad que uno dado. Podemos observar que si se cumple que

                 $nodo1->rgt+1 == $nodo2->lft

podremos asegurar que $nodo1 y $nodo2 están a la misma profundidad. Siguiendo con esta dinámica podremos buscar que nodo cumple que su valor lft es igual a $nodo2->rgt+1 y así sucesivamente para completar toda la lista de nodos al mismo nivel de profundidad.

Vemos que estructurar nuestra información jerarquizada de esta forma, además de ofrecernos información más compacta, nos permite realizar con relativa sencillez multitud de operaciones que con el planteamiento que se presentaba al principio del artículo tendrían cierta complejidad.
Lo mejor de todo es que si analizamos con detenimiento veremos que muchas de estas operaciones las podríamos resolver directamente en SQL sin tener que realizar implementaciones en otro lenguaje, lo cual nos hará ganar en eficiencia.

Para consultar información más precisa, así como implementación de estas operaciones recomiendo acceder al siguiente artículo de Mike Hillyer: Managing Hierarchical Data in MySQL

Prefacio

//-------------THIS IS THE START OF EVERYTHING THAT IS WRONG-------------

Este es un blog de programación web. Aunque el contenido es público su actualización corresponde a la necesidad personal que tengo de de plasmar ideas y conceptos de forma real y práctica, no teórica y académica.
Habitualmente programo en PHP y uso Joomla como gestor de contenidos, además de varias extensiones como Flexicontent o Virtuemart. También, en menor medida, uso Javascript usando JQuery como framework y CSS3, aunque mis labores por el momento no están encaminadas al desarrollo de interfaz de usuario donde estas dos herramientas se usan de forma más intensiva. Sin embargo este es un campo que necesito ampliar con cierta urgencia y por lo tanto espero tratar aquí con no poca frecuencia.
Espero que estas notas que vaya publicando sean útiles para alguien más,  pero nadie debería tomarlas como referencia a seguir ya que, al fin y al cabo, no tengo lecciones que dar, salvo las que cada uno pueda sacar de mis propios tropiezos.